Olemme toteuttaneen Karelia-amk:n tekniikan alojen sekä metsätalouden koulutuksissa matematiikan lähtötasotestin aloittaville ryhmille vuodesta 2022 alkaen. Tänä vuonna mukaan liitettiin liiketalouden aloittavat ryhmät.
Lähtötasotesti uudistettiin syksylle 2024. Testin lähtökohtana on perusasteen yläluokkien matematiikan oppimissisältö. Testi jaettiin kahteen osaan, joista A-osassa testattiin peruslaskutaitoja ja algebran osaamista. B-osiossa keskityttiin soveltaviin tehtäviin painottaen geometrian osaamista. Tässä artikkelissa käsittelemme vain A-osion tuloksia, sillä B-osio vaatii vielä kehittämistä.
Esimerkkejä testin A-osion kysymyksistä

Kaikkien ryhmien tulosten tarkastelua
Tilastollisessa testauksessa käytimme niin sanottuja parametrisia testejä, joiden lähtöoletuksena on, että otokset ovat normaalijakautuneesta perusjoukosta. Anderson-Darling -normaalisuustestin nojalla voidaan olettaa, että kaikki ryhmät ovat peräisin normaalijakautuneesta perusjoukosta (Kangas & Smolander 2022).
Aloitimme tarkastelun tutkimalla kaikkien osallistuneiden pisteiden jakaumaa. Lähtötasotestin A-osion maksimipistemäärä oli 31 pistettä. Kaikkien testiin osallistuneiden opiskelijoiden pistekeskiarvoksi tuli 18,4 pistettä ja 95 %:n luottamusraja oli 17,7–19,0.
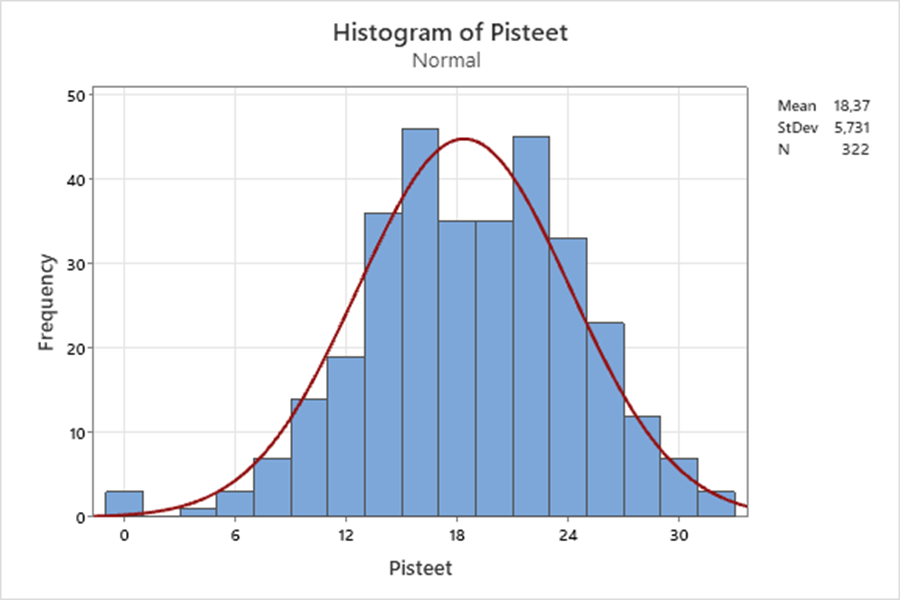
Tulosten tarkastelua koulutusaloittain
Tarkastelimme myös koulutusalojen välisiä eroja.
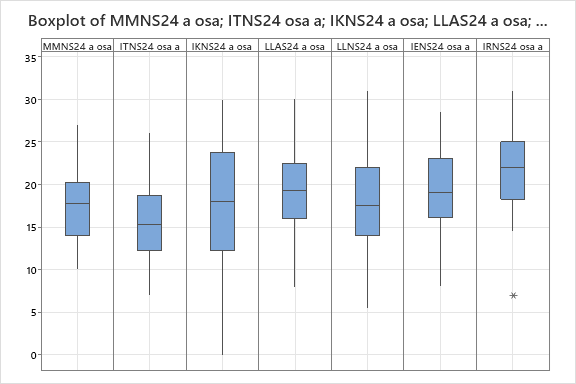
Varianssianalyysin perusteella koulutusalojen pistekeskiarvojen välillä löytyi tilastollisesti erittäin merkitseviä eroja (p-arvo < 0,001). Parivertailun perusteella havaittiin, että ryhmä IRNS24 poikkeaa tilastollisesti merkitsevästi seuraavista ryhmistä: ITNS24, IKNS24, MMNS24 ja LLNS24. Muiden ryhmien välillä parivertailussa ei havaittu tilastollisesti merkitseviä eroja. Kuvassa 3 on esitetty ryhmien pistekeskiarvot ja 95 prosentin luottamusrajat.
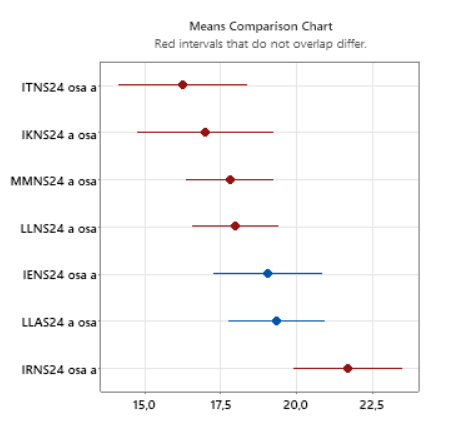
Kokosimme ryhmien keskeisimmät tunnusluvut alla olevaan taulukkoon.
| ITNS24 | IKNS24 | MMNS24 | LLNS24 | IENS24 | LLAS24 | IRNS24 | |
| Keskiarvo | 16,2 | 17,0 | 17,9 | 17,6 | 19,0 | 19,3 | 21,7 |
| Keskihajonta | 5,1 | 7,4 | 4,5 | 5,7 | 5,0 | 4,9 | 5,1 |
| Mediaani | 15,3 | 18,0 | 17,8 | 17,5 | 19,0 | 19,3 | 22 |
| Otoskoko | 28 | 52 | 46 | 77 | 36 | 46 | 37 |
| Vaihteluväli | 7–26 | 0–30 | 10–27 | 5,5–31 | 8–28,5 | 8–30 | 7–31 |
Koulutustaustan vaikutus tuloksiin
Testin taustakysymyksissä selvitettiin vastaajien koulutustaustaa: lukion pitkä matematiikka, lukion lyhyt matematiikka, ammattikoulun matematiikka tai muu.
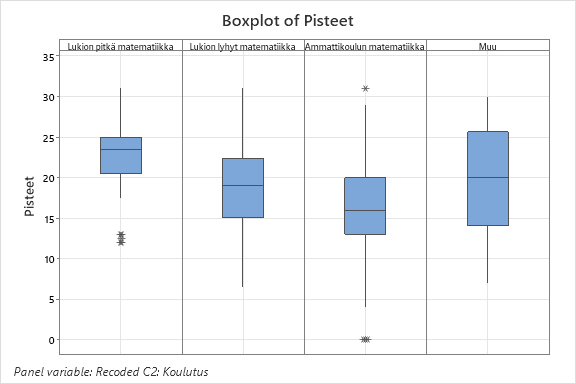
Varianssianalyysin perusteella koulutustaustalla on tilastollisesti erittäin merkitsevä vaikutus pistekeskiarvoon (p-arvo < 0,001). Parivertailun perusteella havaittiin, että ammattikoulutaustaiset poikkeavat tilastollisesti lukion lyhyen ja pitkän matematiikan suorittaneiden tuloksista. Lukion lyhyen matematiikan suorittaneet poikkeavat tilastollisesti ammattikoulun käyneistä ja lukion pitkän matematiikan suorittaneista. Lukion pitkän matematiikan suorittaneet poikkeavat tilastollisesti ammattikoulun ja lyhyen matematiikan suorittaneista. Ryhmä Muu ei poikkea tilastollisesti merkitsevästi mistään ryhmästä.
Pohdintaa
Syksyllä 2024 jatkettiin matematiikan tukipajatoimintaa tekniikan koulutusten osalta. Näihin tukipajoihin osallistui viikoittain noin kymmenen opiskelijaa pääsääntöisesti kone- ja energiatekniikan ryhmistä. Olemme esittäneet, että jatkossa tukitoimet resursoitaisiin opintojakson opettajalle ja varsinaisista matikkapajoista luovuttaisiin. Näin tuki voitaisiin kohdistaa oikea-aikaisesti sitä tarvitseville. Jatkossakin olisi tärkeää tunnistaa heti opintojen alkuvaiheessa ne opiskelijat, jotka hyötyisivät eniten tukitoimista.
Kiitos kaikille kollegoille, jotka mahdollistitte tunneillanne lähtötasotestin suorittamisen!
Kirjoittajat:
Jani Kangas, lehtori, Karelia-ammattikorkeakoulu
Lisbeth Smolander, lehtori, Karelia-ammattikorkeakoulu
Lähteet:
Kangas, J., Smolander, L. 2022. Tekniikan opiskelijoiden matemaattisen osaamisen kehittyminen ensimmäisen opiskeluvuoden aikana. Pulssi 8.5.2022 https://www.karelia.fi/2023/05/tekniikan-opiskelijoiden-matemaattisen-osaamisen-kehittyminen-ensimmaisen-opiskeluvuoden-aikana/

